Union Findで親の頂点番号とグループのサイズを1つのvectorで管理するやつについて
April 16, 2020
前にまとめたのだけど
UnionFindは自分が競技プログラミング初めて、最初に感動したデータ構造だったと思う
UnionFindの仕組みというよりUnionFindの実装方法, データサイズを負の値で管理して1つのvectorで親のidとデータサイズを管理しているとこ
ここを図で説明してみるのがこの記事
UnionFindについては詳しい記事いっぱいあるのでそっちをみた方が良い
UnionFindとは
木が同じグループに属するかの判定などを高速に行えるデータ構造
C++でUnionFindの定義
上記の参考元をベースに自分の理解をコメントで付与したものが以下
struct UnionFind {
/**
* parで親の頂点番号と、サイズを同時に管理する
* 根ではない頂点のparは親となる頂点の値が入ってる
* 根にはサイズ数が入っている。区別できるようにサイズはマイナスの値で入っている
* そのため、初期値はすべて-1になる(mergeの際にmergeされる側の根に、mergeする方の根が加算される)
*/
vector<int> par;
/**
* コンストラクタ
* 最初は全ての頂点が、別グループで初期化する
* @param n : 全ての頂点数
*/
UnionFind(int n) : par(n, -1) { }
/**
* 頂点xが属するグループの根になる頂点の番号を返す
* @param x : 頂点番号
* @return 頂点xが属するグループの根になる頂点の番号
*/
int root(int x) {
// 負の値ということは、根である
if (par[x] < 0) return x;
return par[x] = root(par[x]);
}
/**
* 頂点xとyをマージする(1つのグループにする)
* @param x : マージしたい頂点番号
* @param y : マージしたい頂点番号
* @return Bool値を返す, マージ成功した場合は`true`, すでに同じグループだった場合は`false`を返す
*/
bool merge(int x, int y) {
x = root(x); y = root(y);
if (x == y) return false;
// サイズが大きいほうにマージする
// 以下は必ずxが大きいほう(サイズはマイナスの値が入ってるので)にするように調整している
if (par[x] > par[y]) swap(x, y);
// xのサイズに、yのサイズを加算する
par[x] += par[y];
// yの根をxに更新する
par[y] = x;
return true;
}
/**
* 頂点xとyが同じ木に属するかを判定する
* @param x : 頂点番号
* @param y : 頂点番号
* @return xとyが同じ木に属するのであれば`true`, そうでないのであれば`false`を返す
*/
bool same(int x, int y) {
int rx = root(x);
int ry = root(y);
return rx == ry;
}
/**
* 頂点xが属する木のサイズ(その木に属する頂点の個数)を返す
* @param x : 頂点番号
* @return 頂点xが属する木のサイズ
*/
int size(int x) {
// サイズはマイナスで入ってるので、-をかけて返す
return -par[root(x)];
}
};
親の頂点番号と、サイズを同時に管理する?
これがいまいち理解できなかったので図で可視化してみた
頂点数=7で考える
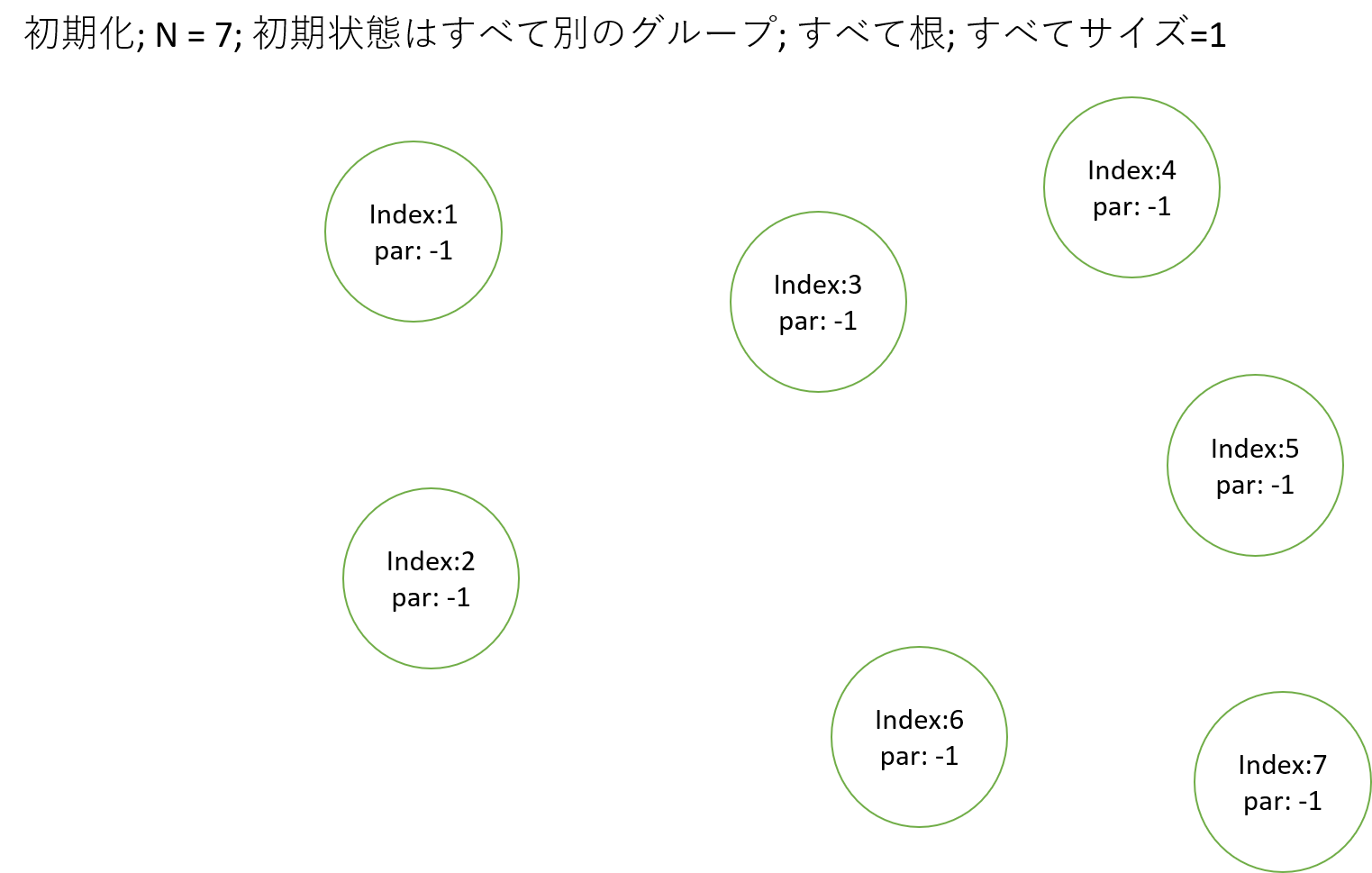
頂点1と4を同じ木に属させるために、merge関数を呼ぶ
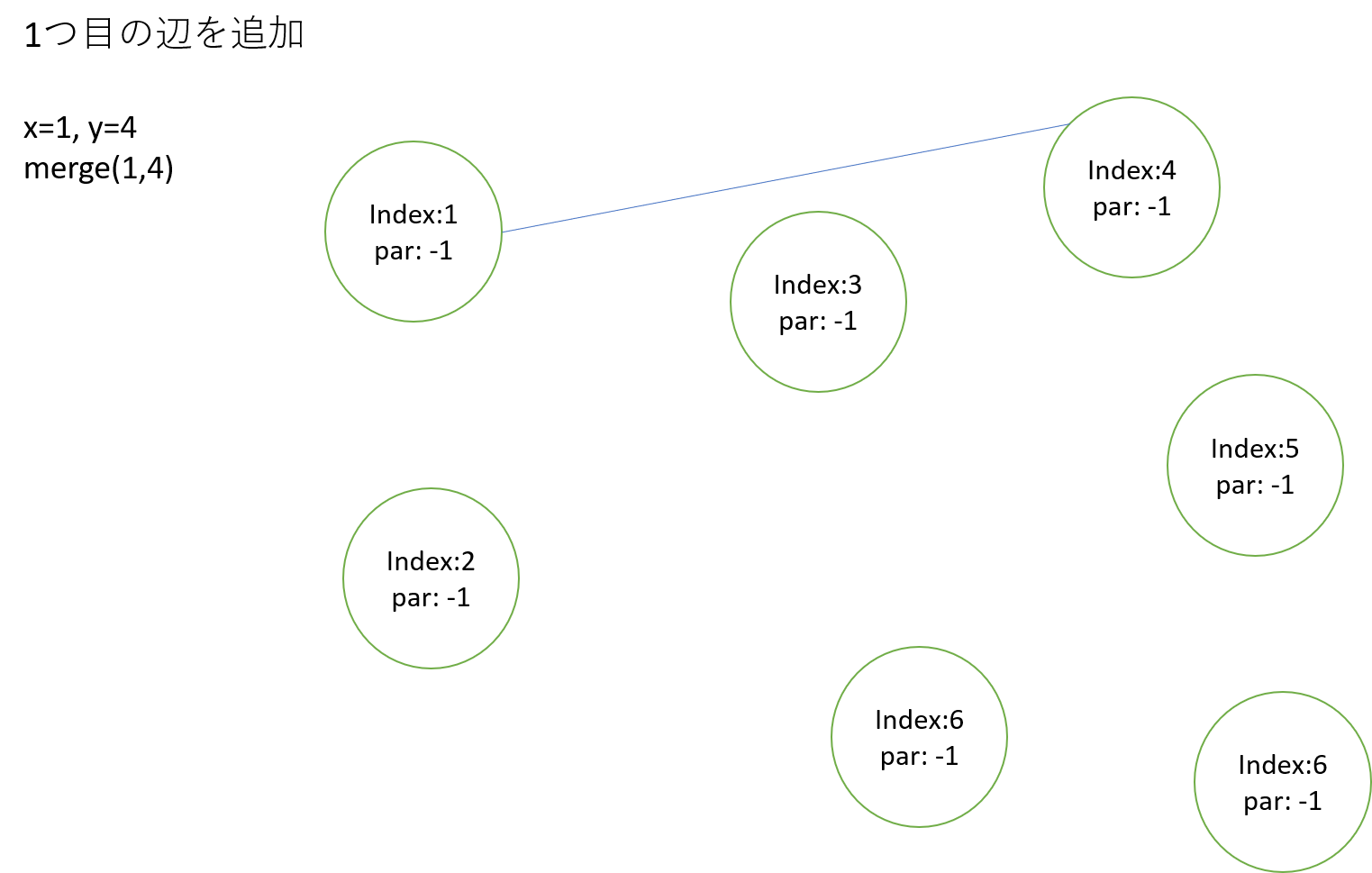
ここではサイズは同じ1なので、xに指定されたindex:1が親となる
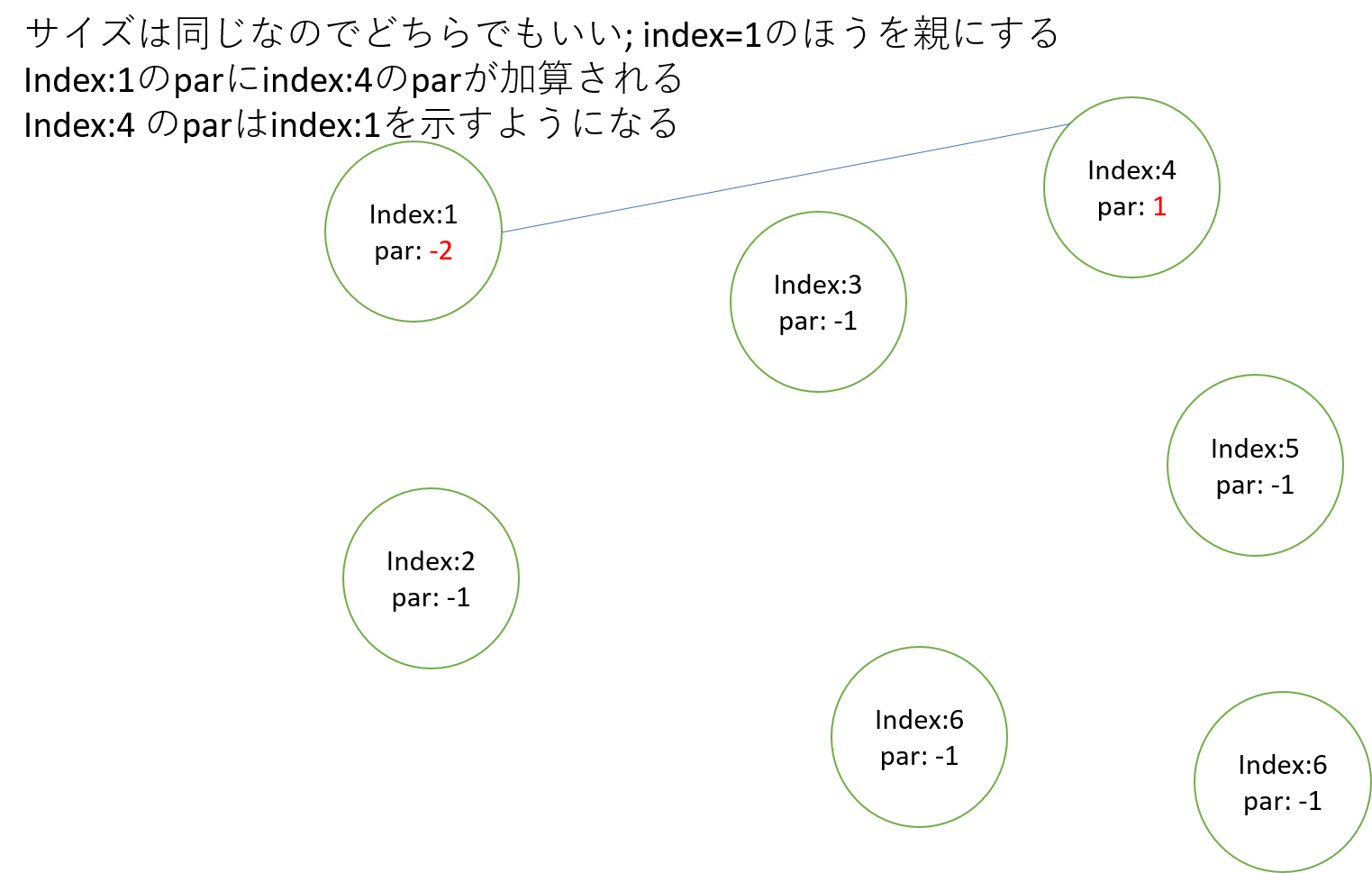
同様に頂点3と5, 頂点2と6をmergeする
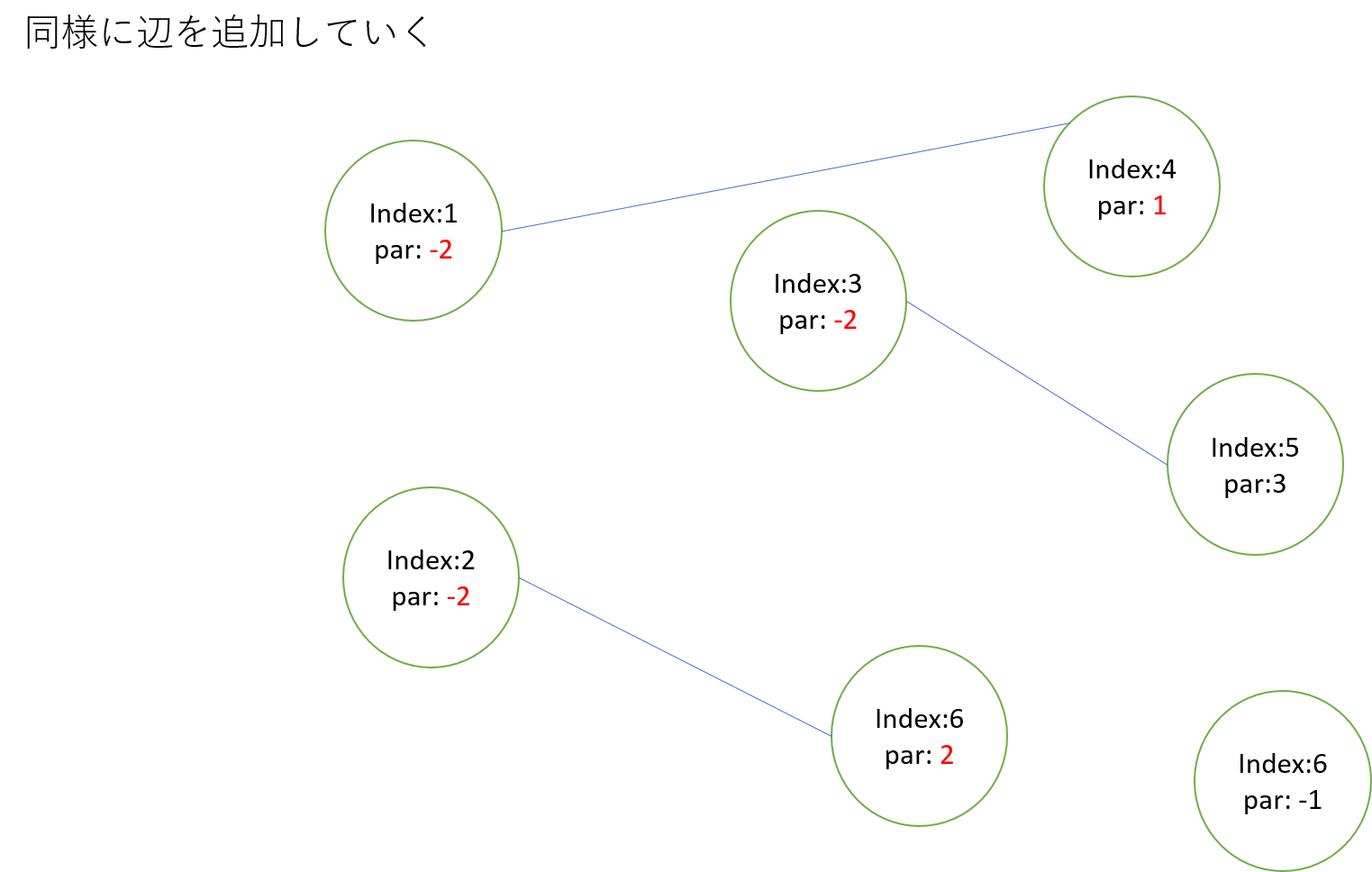
サイズが異なる木をmergeする
頂点1と4が属する木と頂点6をmergeする
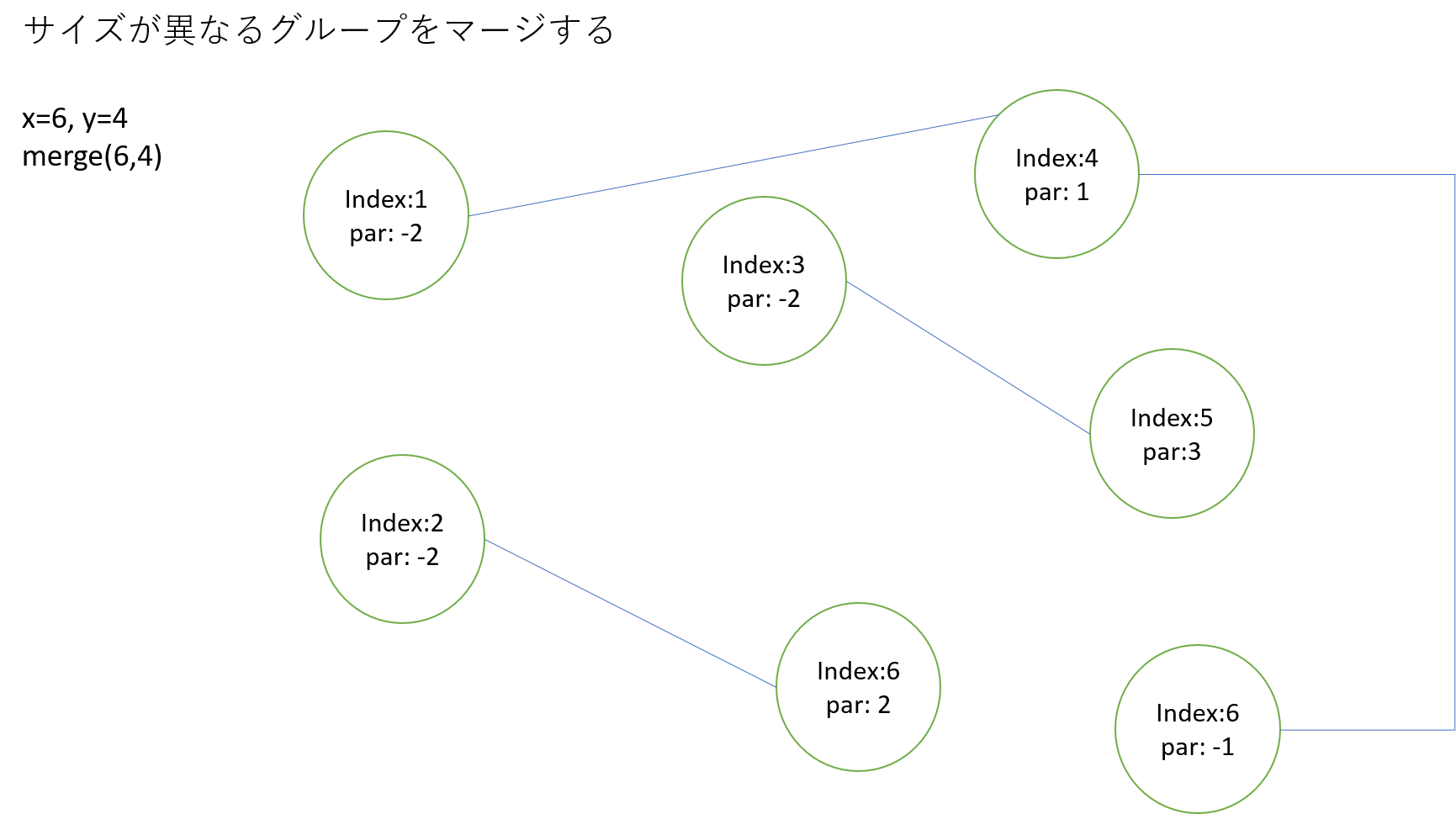
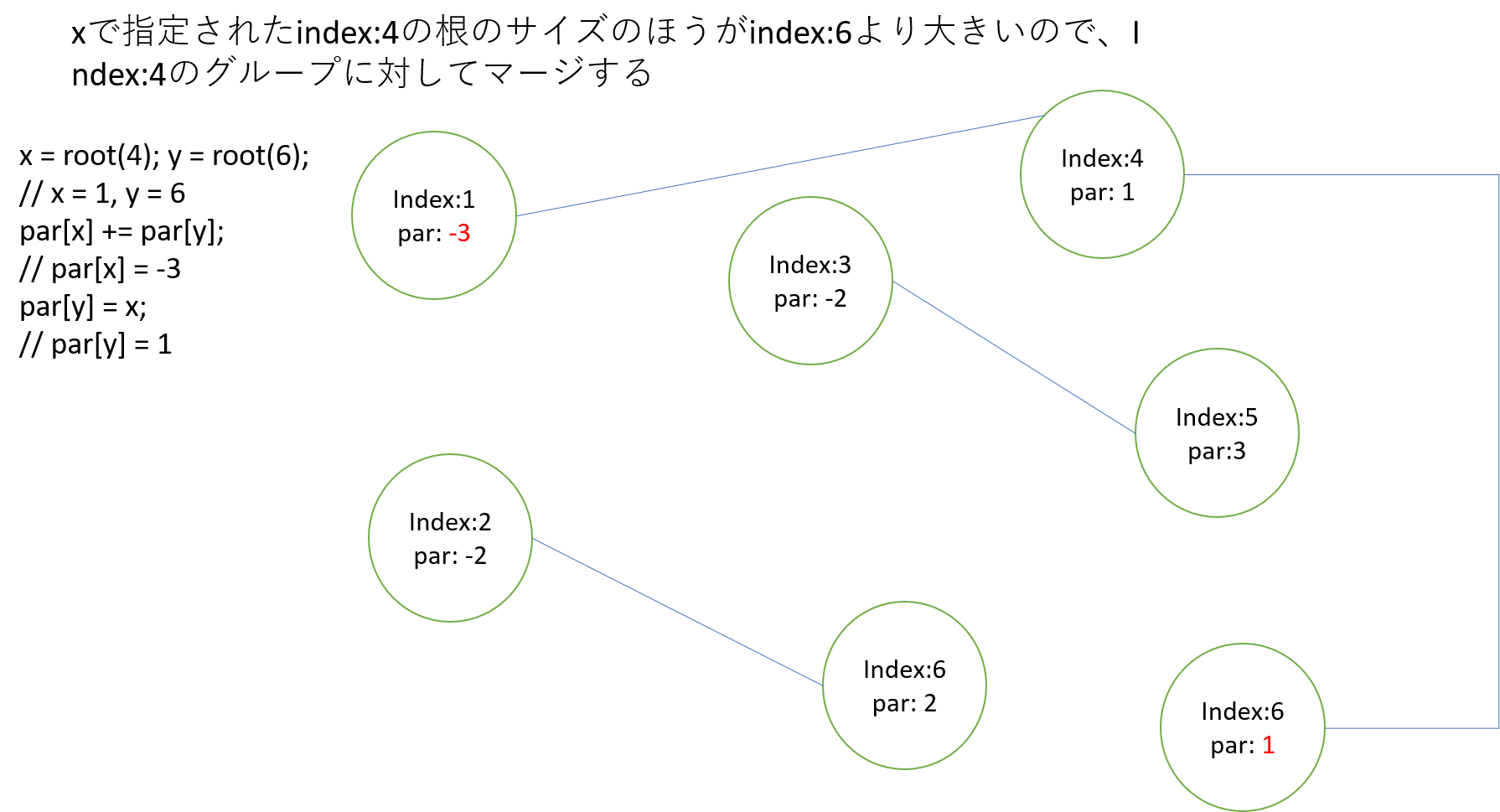
頂点1と4が属する木の方がサイズが大きいので、そちらにmergeされる
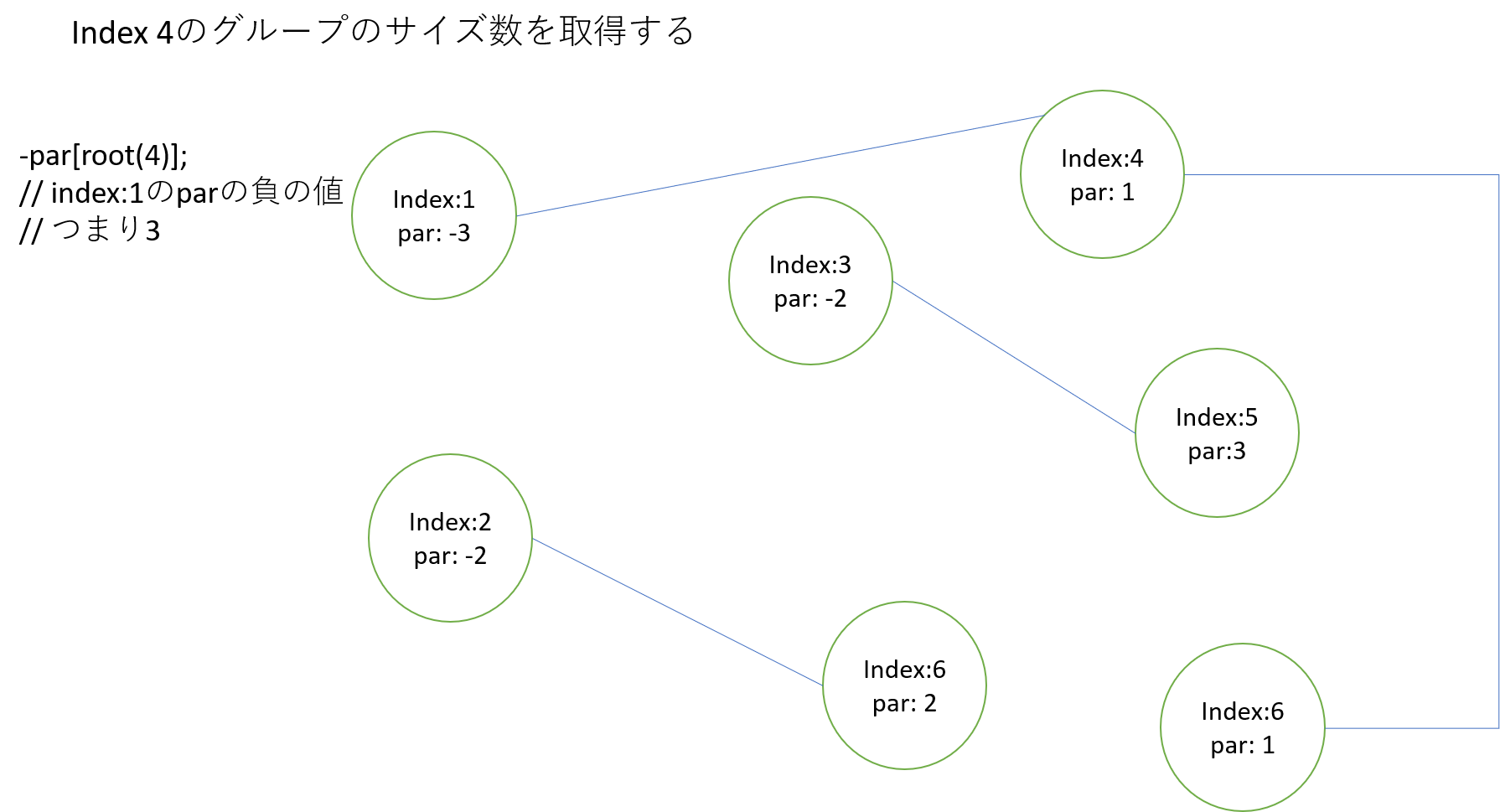
頂点4が属する木のサイズを取得する
頂点4は根が頂点1の木に属するpar[1]の値は-3なので, つまり3つの頂点がこの木に属しているとわかる
AtCoderでUnionFindを使う問題
過去にといた問題
ABC126 E - 1 or 2
基本的なUnionFind問題
問題文からグラフ問題ということが読み解けるかどうかが一番の難所
ABC157 D - Friend Suggestions
友達関係をUnionFindで表現して、計算を高速化する
ABC120 D - Decayed Bridges
自分が初めてUnionFind知った問題
一気にUnionFindを構築せずに、順番に構築したりする